The goal is to add a new visibility badge that indicates the visibility of a Descriptive Phrase’s children which will be referred to Hierarchical Visibility (HV). This badge would be in addition to the badge that controls the visibility of the Descriptive Phrase’s 3D Geometry which will referred to as Geometric Visibility (GV).
GV is binary by nature; however, HV is trinary since all, some, or none of its children could be visible.
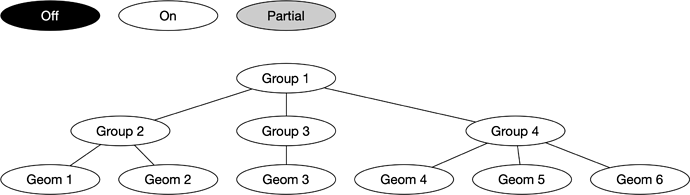
Consider the following example:
In this case, everything is visible. If Geom 1’s visibility is switched off, the resulting HV of the upper nodes should look like this:
If Geom 2 is also switched off, then we would get this:
Calculation of HV
- HV for a Phrase is Visible if all of the contributing HV (CHV)s of its children are Visible.
- HV for a Phrase is Invisible if all of the CHVs of its children are Invisible.
- HV for a Phrase is Partial if any of the CHV of its children is Partial or if some of the children’s CHV are Visible and some are Invisible.
Calculation of a Phrase’s Contributing Hierarchical Visibility (CHV)
- If a Phrase has no children and just geometry, then its CHV is the same as its GV.
- If a Phrase has no geometry and just children, then its CHV is the same as its HV.
- If the Phrase has both then:
- If its GV and HV are both Visible then its CHV is Visible
- If its GV and HV are both Invisible then its CHV is Invisible
- Else its CHV is Partial
Simple Approach
A straightforward implementation would be when a Phrase’s GV or HV is changed, it would then request its parent Phrase to recalculate its HV and then tell its parent Phrase to recalculate and so on. The issue with this approach is that there are a lot of unneeded calculations. Referring to the above example, lets assume Geom 4’s visibility is turned off. Group 4’s HV would become Partial as shown below:
If Geom 6 is then switched off notice that Group 4’s state doesn’t change and would not need to propagate up any further.
Storing Current State
Therefore one performance improvement would be for a Phrase to know its current HV and then compare it when asked to recalculate. If the new state matches its original state then we don’t need to propagate up the tree.
A Phrase’s Visibility Info would consist of the following:
- Number of Children On (unsigned int)
- Number of Children Off (unsigned int)
- Number of Children Partial (unsigned int)
- Has Geometry (bool)
- GV (bool)
Note that we are storing the fact that the Phrase has geometry cause it can be somewhat expensive to determine, while it is cheap to determine if it contains children. This information would be stored as a map on the Descriptive Phase Model for the new visibility badges.
How It Could Work
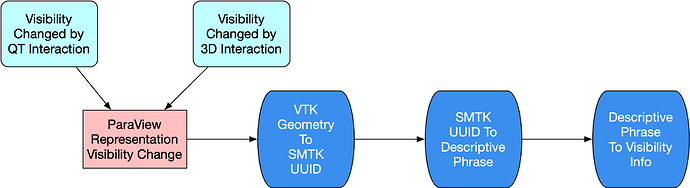
When the user either selects the geometric entities in 3D and triggers their visibility via a keypress or context menu, their corresponding representation in ParaView will have their visibility changed. These representations will get mapped into their SMTK UUIDs which will then be mapped into their Descriptive Phrases via a map stored in the Descriptive Phrase Model. The Visibility Information would then get looked upon for each Phrase, get modified and then propagated up the tree to calculate parent Phrase Visibilities.
If the visibility changes are triggered via QT, then the set of SMTK components effected by the change would be calculated and then their VTK representations would have their visibility changed.
Processing GV Changes
- Look up the Phrase’s Visibility Info
- See if its GV has changed - if it hasn’t there is nothing to do
- Calculate the Phrase’s current and new CHV for its parent Phrase and propagate this information upward
- Parent Phrase determines if its HV has changed, if not there is nothing more to do
- Calculate its change in CHV and propagate it upward
Processing HV Changes
- Calculate the Phrase’s descendants which contain GV’s and whose GV would be changed
- Process these GV Changes
Note!
As you can see, this process assumes that the entire Phrase Tree has been created since we need to use the children information when determining GV changes caused by HV changes. And we need the parent information when updating HV state caused by GV changes.